All A are B
No A are B
No B are A
No B are A
Some A are B
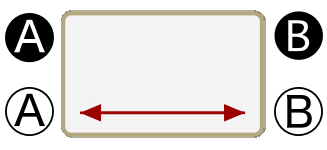
Some B are A
Some B are A
Some A are not B
There are three additional but equivalent ways of expressing what each of the four basic sentence forms asserts. For starters, "Some A are B" is equivalent to "Some B are A" because both expressions assert the very same thing, viz., they assert that category A and category B have membership in common. It is standard to interpret "some" to mean "at least one," so both expressions assert that categories A and B have at least one member in common.Note 1 Likewise, "No A are B" and "No B are A" equivalently express that the two categories, A and B, have no member in common. Conversion is the name of this process of switching the subject and predicate terms and so, for example, "Some dogs are pets" and "Some pets are dogs" are equivalent converses of each other, as are "No dogs are cats" and "No cats are dogs." Whenever sentences are equivalent if one of them is true the other is true also, and if one is false then so is the other.
Now "All A are B" and "Some A are not B" cannot be equivalently converted. For example, "All poodles are dogs" is not equivalent to "All dogs are poodles" since the former is true and the latter is false; and the same is the case with "Some dogs are not poodles" and "Some poodles are not dogs."
To impose these statements onto the schematics we first represent A and B as A and B on a lower line and then represent nonA and nonB as A and B above them to form the corners of a rectangle. Then on each rectangle these terms are connected by red or green, single-ended or double-ended arrows to display the four equivalent statements on each rectangle.
To do this we let green arrows between terms indicate affirmative sentence forms (viz.., "All A are B" and "Some A are B") while we let the red arrows between terms indicate the negative forms (viz., "No A are B" and "Some A are not B"); and we let double-ended arrows represent convertible sentence forms (viz., "Some A are B" and "No A are B") and single-ended arrows represent nonconvertible forms (viz., "All A are B" and "Some A are not B"). Accordingly, the original statements and their equivalents considered so far appear below where the statement of each sentence form is given beneath its arrow and the two equivalent converse statements are given beneath the double-ended arrows (where each arrowhead represents one of them):
Now in order to complete all the equivalences for each of the four statement forms, the complementary terms, nonA and nonB, must be referred to.
These four schematics are completed in the first group below where the equivalent sentence forms are listed below the rectangle of arrows that represent them. Note that these schematics are also given in the top row of "cards" on the opening screen of ReasonLines and when any card is clicked or tapped there the statement forms listed below its schematic here will also appear there.