Study Tips

  1. Study each statement form below a schematic until you see how each is equivalent to the three others. Using real categories for the variables may prove helpful; for example, think: "if All poodles are dogs, then necessarily No poodles are nondogs; then since No poodles are nondogs it follows that No nondogs are poodles (conversion); then since No nondogs are poodles, All nondogs have to be nonpoodles" See it? Then think through the others the same way.
  2. Make sure to relate each statement to the arrow of the schematic that represents it. There will then be no need to memorize all the forms because they can be read off the schematics.

All A are B
No A are B
No B are A
All B are A
All A are B
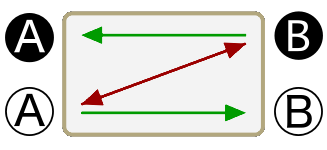
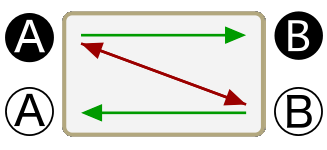
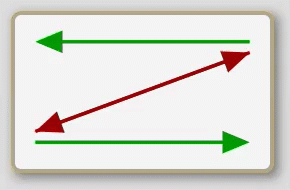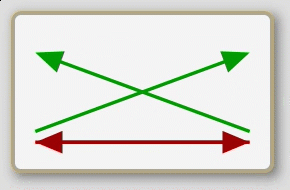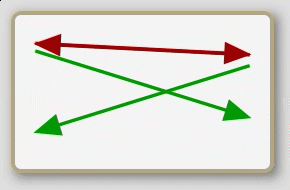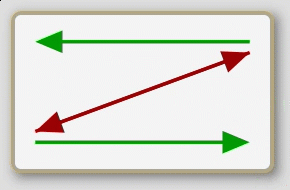
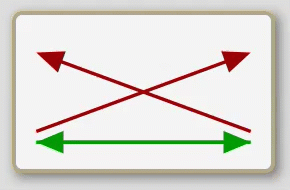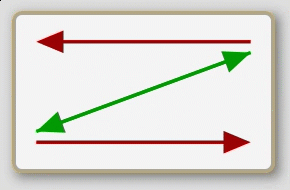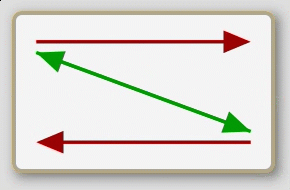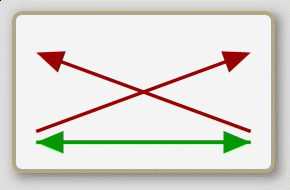
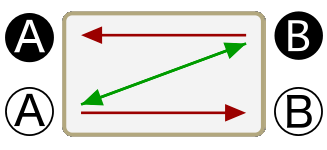
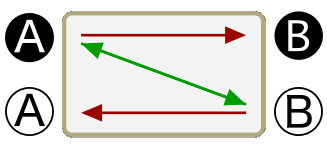
No A are B
No B are A
All B are A
Some A are not B
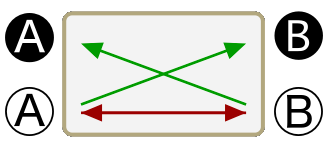
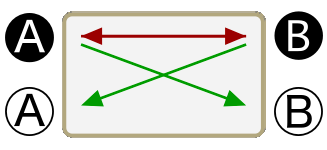
Some A are B
Some B are A
Some B are not A
Some A are not B
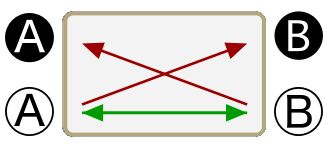
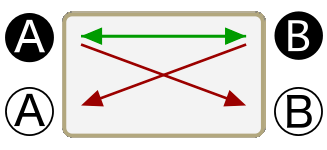
Some A are B
Some B are A
Some B are not A

But these four schematics are only half of the total for none of their statement forms has A as its subject term. Note 2 The remaining ones are given below, and they also appear as the bottom row of cards on the opening screen of ReasonLines.

All A are B
No A are B
No B are A
All B are A
All A are B
No A are B
No B are A
All B are A
Some A are B
Some B are A
Some A are not B
Some B are not A
Some A are not B
Some A are B
Some B are A
Some B are not A

There are 32 individual sentence forms given here and each is schematized by one arrow, or by one point of a double-ended arrow; however, there are only eight distinct arrangements of arrows and I shall refer to these arrangements as schematics of the eight "proposition forms." For example, when the following content is given to "All A are B" and its equivalents I shall say that

All poodles are dogs,
No poodles are nondogs,
No nondogs are poodles, and
All nondogs are nonpoodles

are four different sentences which assert one and the same proposition. That is, although they are four distinct expressions they each assert that the very same thing is the case.

The eight propositions are not named in the traditional logic; rather, the traditional treatment deals exclusively with the individual sentences. So for lack of a historical precedent I shall refer to the eight, whole propositions here by their schematic characteristics. First, note that the arrows of the second row of schematics are exactly the same as those of the first row flipped down. (This may be more evident on the opening screen of the app than it is above.) Second, note that each schematic is either predominately red (with two red arrows to one green arrow) or predominately green (with two green arrows to one red arrow); and also, note that each either has a basic x-shape or z-shape. Now, if we consider the orientation of the first row of schematics to be upright we can call them, from left to right, up- green-z, up-green-x, up-red-x, and up-red-z; then the second row becomes, from left to right, down-green-z, down-green-x, down-red-x, and down-red-z.

(With these names one may become able to visualize the schematics and then "read" the four sentence forms from the images.)

Finally, I think it is worth noting that the left four schematics—two up and two down—are predominately green. They are all composed of one double-ended, red arrow in the middle with a green, single-ended arrow hinged to each tip. If we think of these as physical objects we can picture how the hinges would allow them to be folded into either an x-shape or a z-shape, and then they could be flipped vertically to produces all four representations of the universal statements. Likewise, the four right schematics are predominately red; that is, they have a green double-ended arrow in the middle which is flanked by single-ended red arrows. In like fashion we can picture them folded into an x-shape or a z-shape and flipped vertically to yield all four representations of particular statements.

Click/tap on image to play animation.
Footnotes
Note 2
Perhaps it is worth noting that while A is just as fine a subject term as A in abstract logic, in ordinary conversation it is normally only used in "limited domains of discourse"; for example, since "nonpoodles" covers literally everything that is not a poodle (including rainbows, quasars, molecules, poems, etc., etc.,), it would seem difficult to make a meaningful statement about this subject. However, at a dog show the owners might naturally talk about nonpoodles because here the domain of discourse would be limited to breeds of dogs; or the principal might speak freely about nonseniors because here the domain would be limited to the students at the school. Etc.